Муниципальное учреждение

«Управление образования администрации

городского округа Прохладный, КБР»

 

 

IV Городская научная конференция учащихся

«Человек. Природа. Техника»

 

 

 

Секция: «Математика»

 

 

 

 

 

Автор

ученица 6 «А» класса

МОУ «СОШ №4»

Шишкова Алина

Руководитель:

учитель математики

МОУ «СОШ №4»

Шишлова Вера Владимировна

 

 

 

 

 

г. Прохладный

2009-2010 уч. год

Оглавление

 

I. Введение.

II.         Основная часть.

III.      Заключение.

IV.     Список литературы.

I. Введение

    Решениям задач уделяется достаточно много внимания в VI—IX классах средней школы. Умение решать задачи современный человек независимо от рода деятельности и уровня образования нуждается непрерывно. Без умения решать задачи  нельзя обойтись ни в финансовом анализе, ни в статистике. Чтобы начислить зарплату работнику нужно знать процент налоговых отчислений; чтобы открыть депозитный счет в сбербанке мы интересуемся размером процентных начислений на сумму вклада; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции. В торговле понятие процент используется наиболее часто: скидки, наценки, уценки, прибыль, кредит, налог на прибыль и т.д. Россию захватил «кредитный бум»: в наше время люди все чаще берут кредит на приобретение жилья, автомобиля, потребительские кредиты и кредит на образование.

 Кроме того, очень часто встречаются  задачи, в которых  нужно уметь решать задачи не только на проценты, но и другие.

Учитывая актуальность данной темы, нами проведена данная исследовательская работа.

1.1.Цель исследования -  математическая классификация типичных вопросов способов решения задач.  

1.2.Предмет исследования- способы решения задач, включенные в школьные учебники, сборники задач.

1.3.Гипотеза исследования – знание типов задач, и умение переводить условие задачи на умение ее решать.

Цель, предмет и гипотеза исследования обусловили выдвижение и решение следующих задач исследования:

·       Изучить теоретический материал по данной теме

·       Проанализировать тексты задач из учебников и задачников для средней школы.

II. Основная часть 

2.1. Способы решения текстовых задач.

               Общепризнанно, что для выработки у учащихся умения решать задачи, важна всесторонняя работа над одной задачей, в частности, и решение её различными способами.

               Следует отметить, что решение задач различными способами позволяет убедиться в правильности решения задачи даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче.

Возможность решения некоторых задач разными способами основана на различных свойствах действий или вытекающих из них правил.

               При решении задач различными способами ученик привлекает 

дополнительную информацию, поскольку он непроизвольно выполняет в большем числе выборы суждений, хода мысли из нескольких возможных; рассматривается один и тот же вопрос с разных точек зрения. При этом полнее используется активность учащихся, прочнее и сознательнее запоминается материал. Как правило, различными способами решается  те из задач, где этого требует вопрос, поэтому такая работа носит эпизодический характер.

               В качестве основных в математике различают арифметический и алгебраический способы решения задач. При арифметическом способе ответ на вопрос задачи находится в результате выполнения арифметических действий над числами.

               Арифметические способы решения задач отличаются друг от друга одним или несколькими действиями или количеством действий, также отношениями между данными, данными и искомым, данными и неизвестным, положенными в основу выбора арифметических действий, или последовательностью использования этих отношений при выборе действий.

               При алгебраическом способе ответ на вопрос задачи находится в результате составления и решения уравнения.

               В зависимости от выбора неизвестного для обозначения буквой, от хода рассуждений можно составить различные уравнения по одной и той же задаче. В этом случае можно говорить о различных алгебраических решениях этой задачи.

               Но надо отметить, что в начальных классах алгебраический способ не применяется для решения задач.

               Опираясь только на чертёж, легко можно дать ответ на вопрос задачи. Такой способ решения называется графическим.

               До настоящего времени вопрос о графическом способе решения арифметических задач не нашёл должного применения в школьной практике.

Графический способ даёт возможность более тесно установить связь между

арифметическим и геометрическим материалами, развить функциональное мышление детей.

               Следует отметить, что благодаря применению графического способа в начальной школе можно сократить сроки, в течение которых ученик научится решать различные задачи. В то же время умение графически решать задачу – это важное политехническое умение.

               Графический способ даёт иногда возможность ответить на вопрос такой задачи, которую дети ещё не могут решить арифметическим способом и которую можно предлагать во внеклассной работе.

               Решение задач различными способами – дело непростое, требующая глубоких математических знаний, умения отыскивать наиболее рациональные решения.

2.2. Этапы решения задач.

Решение текстовых задач – это сложная деятельность, содержание которой зависит как от конкретной задачи, так и от умений решающего. Тем не менее, в ней можно выделить несколько этапов:

1.   Ознакомление с содержанием задачи;

2.   Поиск решения задачи;

3.   Выполнение решения задачи;

4.   Проверка решения задачи.

Выделенные этапы органически связанны между собой, и работа на каждом этапе ведётся на этой ступени преимущественно под руководством учителя.

Ознакомиться с содержанием задачи – значит, прочитав её, представить жизненную ситуацию, отраженную в задаче. Читают задачу, как правило, дети.

Очень важно научить детей правильно читать задачу: делать ударение на числовых данных и на словах, которые определяют выбор действия, таких, как «было», «уехали», «осталось», «стало поровну» и т.п., выделять интонацией вопрос задачи.

Задачу дети читают один – два, а иногда и большее число раз, но постепенно их надо приучать к запоминанию задачи с одного чтения, так как в этом случае они будут сразу читать задачу более сосредоточенно.

               После ознакомления с содержанием задачи можно приступить к поиску её решения: ученики должны выделить величины, входящие в задачу; данные и искомые числа, установить связи между данными и искомым и на этой основе выбрать соответствующие арифметические действия.

               Выделяются несколько приёмов поиска решения задачи.

               Иллюстрация задачи – это использование средств наглядности для выявления величин, входящих в задачу, данных и искомых чисел, а также для установления связей между ними.

Иллюстрация может быть предметной и схематической. В первом случае

используются для иллюстрации либо предметы, либо рисунки предметов, о которых идёт речь в задаче: с их помощью иллюстрируется конкретное содержание задачи.

               Предметная иллюстрация помогает создать яркое представление той жизненной ситуации, которая описывается в задаче, что в дальнейшем послужит отправным моментом для выбора действия. Предметной иллюстрацией пользуются только при ознакомлении с решением задачи нового вида и преимущественно в 1 классе.

               Начиная с 1 класса, используется и схематическая – это краткая запись задачи.

В краткой записи фиксируются в удобообразной форме величины, числа данные и искомые, а также некоторые слова, показывающие, о чём говорится в задаче:

«было», «положим», «стало» и т.п., и слова, обозначающие отношения: «больше», «меньше», «одинаковая» и т.п.

               Краткую запись задачи можно выполнять в таблице и без неё, а также в форме чертежа.

               Иллюстрацию в виде чертежа целесообразно использовать при решении задач, в которых даны отношения значений величин (больше, меньше, столько же), а также при решении задач, связанных сдвижением. При этом надо соблюдать указанные в условии отношения: большее расстояние изображать большим отрезком.

               Чертеж наглядно иллюстрирует отношение значений величин, а в задачах на движение схематически изображает соответствующую ситуацию.

Любая из названных иллюстраций только тогда поможет ученикам найти решение, когда её выполняют сами дети, поскольку только в этом случае они будут анализировать задачу сами.

               Дети могут установить связи между данными и искомым и выбрать соответствующее арифметическое действие только с помощью учителя. В этом случае учитель проводит специальную беседу, которая называется разбором задачи.

               При разборе задачи нового вида учитель должен в каждом отдельном случае поставить детям вопросы так, чтобы навести их на правильный или осознанный выбор арифметических действий.

               Очень важно чтобы вопросы не были подсказывающими, а вели бы к самостоятельному нахождению пути решения задачи.

 Разбор задачи заканчивается составлением плана решения.

 План решения – это объяснение того, что узнаём, выполнив то или иное действие, и указания по порядку арифметических действий.

               Часто при введении задач нового вида ученики затрудняются самостоятельно составить план решения, тогда им помогает учитель.

               В этом случае рассуждение можно строить двумя способами: идти от вопроса задачи к числовым данным или от числовых данных идти к вопросу.

Решение задачи – это выполнение арифметических действий, выбранных при составлении плана решения. При этом обязательны пояснения, что находим, выполняя каждое действие.

               Решение задачи может выполняться устно и письменно. При устном решении соответствующие арифметические действия и пояснения выполняются устно.

               Решение почти половины всех задач должно выполняться в начальных классах устно. При этом надо учить детей правильно и кратко давать пояснения к выполненным действиям.

               Проверить решение задачи – значит установить, что оно правильно или ошибочно.

               В начальных классах используются четыре вида проверки:

1. Составление и решение обратной задачи. Если при решении обратной задачи в результате получится число, которое было известно в данной задаче, то можно считать, что данная задача решена правильно.

Он применим к любой задаче, лишь бы обратная задача была посильна детям, а поэтому им надо указывать, какое число можно брать искомым в обратной задаче.

2. Установления соответствия между числами, полученными в результате решения задачи и данными числами. При проверке решения задачи этим способом выполняют арифметические действия над числами, которые получаются в ответе на вопрос задачи, если при этом получатся числа, данные в условии задачи, то можно считать, что задача решена правильно.

               Его целесообразно применять для проверки решения задач такой структуры, в которых можно получить числа, данные в задаче, путём выполнения соответствующих действий над числами, полученными в ответе.

3.   Решение задачи другим способом.

Если задачу можно решить различными способами, то получение одинаковых результатов подтверждает, что задача решена правильно. Два способа нельзя считать различными, если они отличаются только порядком выполнения действий.

4.   Прикидка ответа.

Применение этого способа состоит в том, что до решения задачи устанавливается область значений искомого числа, т.е. устанавливается, больше или меньше какого-то из данных чисел должно быть искомое число. После решения задачи определяется, соответствует ли полученный результат установленной области значений, если он не соответствует установленным границам, значит, задача решена неправильно.

Таким образом, этот способ помогает заметить ошибочность решения, но он не исключает других способов проверки решения задач.

 

2.3. Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Задача

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок - это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Например.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Практический способ.

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

пойманных рыб: л - лещи, о - окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

Арифметический способ

1) 3 + 4 = 7 (р.) - пойманные рыбы

2) 10-7=3 (р.) - щуки

Для ответа на вопрос задачи мы выполнили два действия.

Алгебраический способ

Пусть х - пойманные щуки

Тогда количество всех рыб можно записать выражением:

3 + 4 + х - все рыбы

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Графический способ

•—л—• •—л—• •—л—• •—ок—• •—ок—• •—ок—• •—ок—• •—щ—• •—щ—• •—щ—•

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

Например.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

1) 28 - 12 = 40 (к.)

2) 90 - 40 = 50 (к.)

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

2) 90 - 10 = 50 (к.) на 3 полке.

Ответ: 50 книг.

в) с вопросами

1) Сколько книг на первой и второй полках вместе?

28 + 12 = 40 (к.)

2) Сколько книг на третьей полке?

90 - 40 = 50 (к.)

Ответ: 50 книг.

г) выражением

90 - (28 + 12)

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 - (28 + 12) = 50 (к.)

Ответ: 50 книг.

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 - 28 = 62 (к.) на 2 и3 полках.

2) 62 - 12 = 50 (к.) на 3 полке.

Ответ: 50 книг.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 - 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

Ответ: 50 книг.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Например.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Осталось •——•

Было •——••—1—••—8—•

1) 18 : 2 = 9(м)

2) 9 • 3 = 27(м.)

Ответ: 27 машин было в гараже

Или

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

Раскрасил •——• •——•

Осталось •——•

48 : 3 = 16 (л.) Ответ: 16 листов

 

Существует много способов решения задач. Одни из них знакомы и нам. Это арифметический, алгебраический и графический способы. Но есть и еще один - табличный.

 

арифметический способ.

Этот способ также называют «способом решения задач по вопросам».

Например:

Задача: катер проплыл по озеру за 2 часа 48 километров, а против течения реки за 2 часа он проплыл 46 километров. Какова скорость течения реки?

Возникает вопрос. Сколько катер проплывет за час по озеру?

Выполняется действие:

1)    48:2=24 (км/ч) скорость катера по озеру.

Возникает вопрос. Сколько катер проплывет против течения реки? Выполняется действие:

2)    46:2=23 (км/ч) скорость катера против течения реки.

Раз, у нас есть скорость катера по озеру (то есть скорость катера в стоячей воде) и скорость катера против течения реки, значит, мы можем найти скорость течения реки. Выполняется действие:

3)24-23=1 (км/ч) скорость течения реки. Пишется ответ: Ответ: 1 (км/ч).

 

алгебраический способ.

Это способ решения задач уравнением.

Например:

Задача: мама старше Ани в 5 раз, а бабушка старше Ани в 9 раз. Вместе им 90 лет. Найдите возраст каждой

Нужно составить уравнение. Чтобы это сделать, надо написать условье составление уравнения.

Пишем:

Пусть х возраст Ани, тогда 5х возраст мамы и 9х возраст бабушки. Зная, что им вместе 90 лет составим и решим уравнение.

Составляем и решаем уравнение: х+5х+9х=90 15х=90 х=90:15 х=6

Мы нашли возраст Ани. Но этого нам мало, нужно найти возраст бабушки и мамы. Найдя это, мы сможем решить задачу.

Зная, что возраст мамы в 5 раз больше возраста Ани,

Выполняем действие:

1)  6*5=30 (лет) возраст мамы

Зная, что возраст бабушки в 9 раз больше возраста Ани, Выполняем действие:

2)  6*9=54 (года) возраст бабушки.
Пишем ответ:

Ответ: 6 лет Ани, 30 Маме и 54 года бабушке.

 

Графический способ.

Рисуется чертеж.

Например:

Задача: на гору ведут 5 дорог. Сколькими способами можно выбрать маршрут для того, чтобы подняться в гору и затем спуститься с нее? (обратите внимание: подниматься и опускаться можно по одной и той же дороге.)

Делаем чертеж:

Поскольку мы знаем, что на гору и с горы ведут 5 дорог.

 

На гору                                                            с горы

Считаем, сколько получилось путей. Получилось 25.      Пишем ответ. Ответ: 25 маршрутов.

 

табличный способ.

Такой способ очень похож на таблицу умножения.

Например:

 

Задача. У Васи 20 конфет, а у Димы 16. Сколько у них вместе конфет?

Составляем план таблицы:

План таблицы.

Сверху будет количество конфет у Васи, а слева конфет у Димы.

Чертим таблицу:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26
7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27
8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29
10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32
13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33
14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38
19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39
20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40

 

                                                                                                                         

Сверху находим 20. Слева находим 16. Ведем, пока не пересекутся. Пересеклись в точке 36.

Значит и ответ будет 36. Пишем ответ: Ответ: 36 конфет. Такими способами можно решать задачи.

 

арифметический, по действиям.

         Например:

         Двое фермеров привезли на рынок 180 кг яблок. Первый фермер продал утром  всех яблок, а вечером  всех яблок. Второй фермер также продал утром  всех яблок, а вечером  он продал  оставшихся яблок. Сколько  килограммов яблок  продал каждый фермер за весь день?

Решение:

1. (части) продал 1 фермер утром.

2.  (кг) продал 1 фермер.

3. (части) осталось продать.

4.  (части) продал 2 фермер вечером.

5.  (части) продал 2 фермер за день.

6. (кг) продал 2 фермер.

Ответ: первый фермер продал больше второго.

 

      В двух бочках 64 л. воды. Если из одной бочки перелить в другую 6л, то количество воды в обеих бочках сравняется. Сколько воды в каждой бочке?

1) (64+12):2 = 38 (л) в первой бочке.

2) 64 – 38 = 26 (л) во второй бочке.

Ответ: 38 л, 26 л.

 

 

Это способ алгебраический, то есть  уравнением.

Например:

      В саду яблоневые и грушевые деревья, причем яблоневых было на 54 дерева больше, чем грушевых. После того, как садовник посадил еще 7 яблоневых и столько же грушевых деревьев, яблоневых стало в 4 раза больше грушевых. Сколько было деревьев каждого вида вначале?

      Пусть х будет грушевых деревьев, тогда (х + 54) дерева яблоневых. Составим и решим уравнение:

            (7 + х) 4 = х + 54 + 7

            28 + 4х = х + 61

            4х – х = 61 – 28

            3х = 33

            х = 33 : 3

            х = 11

      Значит 11 грушевых деревьев, тогда 11 + 54 = 65 яблоневых

      Ответ: 11, 65.

 

      В шкафу стоят учебники физики и учебники  химии – всего 112 книг. При этом  учебники  химии составляют  числа учебников физики. Сколько в шкафу учебников по каждому из этих предметов?

      Пусть х будет учебников  физики, тогда х учебников химии. Всего учебников 112. Составим и решим уравнение:

            х + х = 112

           

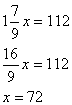
Значит 72 учебника по физике, то 112-72=40 учебников по химии.

Ответ: 72, 40.

 

Это способ комбинаторный, то есть чертежом.

Например:

            На почте  продаются 5 видов поздравительных открыток. Катя хочет купить две различные поздравительные открытки. Сколькими способами она может выбрать две открытки из пяти?

 

                        1          2          3          4          5

 

            1 и 2               2 и 3               3 и 4               4 и 5

            1 и 3               2 и 4               3 и 5

            1 и 4               2 и 5

            1 и 5

Ответ: 10 способами.

 

Это способ подбора или рассуждения.

Например:

            В стаде верблюдов есть одногорбые и двугорбые. На вопрос сколько в стаде одногорбых и сколько двугорбых верблюдов хозяин ответил, что всего в стаде 72  головы и 104 горба. Сколько в стаде одногорбых и двугорбых верблюдов?

Рассуждаем так:

            Каждый верблюд имеет по одному горбу, значит 72 горба. Из 104 вычитаем 72, получаем 32 горба, т.е. 32 верблюда двугорбые, тогда из 72 вычесть 32 получим 40 одногорбых верблюдов. 

 

Ответ: 40 одногорбых и 32 двугорбых

 

            70 туристов разместились в 33 байдарках, среди которых были двухместные и трехместные. Сколько было одноместных байдарок  и сколько трехместных?

            Рассуждаем так:

            Если посадим по 2 туриста в 33 байдарки, получим 66 туристов. Вычтем из 70 66 туристов, остается 4 туриста, и эти  4 туриста рассаживаем в трехместные байдарки. Значит, было 4 трехместных байдарок и 33 – 4 = 29 байдарок двухместных.

 

            Ответ: 29 байдарок, 4 байдарки.

III. Заключение

 

        

С математической точки зрения раздел способов решения задач  в школьной математике является простейшим. Однако в текстовых задачах встречаются такие задачи, которые требуют умение применять различные способы их решения.

Научить быстро, решать задачи  способствует применению различных способов  их решения.  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

IV. Список литературы

 

 

1. Россия. Энциклопедический словарь Брокгауза и Ефрона. — Лениздат, 1991.

2. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4—8 кл. сред. шк. — 5-е изд. — М.: Просвещение, 1988.

3. А.Г. Ванцян «Математика» 5 класс. М.: Просвещение, 2009 г.